source: https://leetcode.com/problems/longest-zigzag-path-in-a-binary-tree/description/
Longest ZigZag Path in a Binary Tree
You are given the root of a binary tree.
A ZigZag path for a binary tree is defined as follow:
- Choose any node in the binary tree and a direction (right or left).
- If the current direction is right, move to the right child of the current node; otherwise, move to the left child.
- Change the direction from right to left or from left to right.
- Repeat the second and third steps until you can’t move in the tree.
Zigzag length is defined as the number of nodes visited – 1. (A single node has a length of 0).
Return the longest ZigZag path contained in that tree.
Example 1:
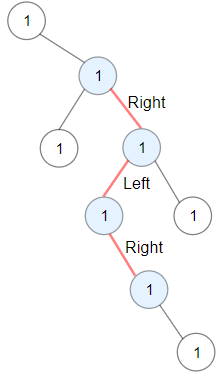
Input: root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1]
Output: 3
Explanation: Longest ZigZag path in blue nodes (right -> left -> right).
Example 2:
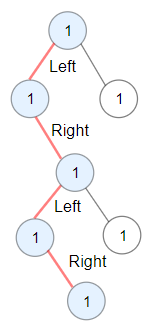
Input: root = [1,1,1,null,1,null,null,1,1,null,1]
Output: 4
Explanation: Longest ZigZag path in blue nodes (left -> right -> left -> right).
Example 3:
Input: root = [1]
Output: 0
Constraints:
- The number of nodes in the tree is in the range [1, 5 * 104].
- 1 <= Node.val <= 100
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public int longestZigZag(TreeNode root) { return Math.max(dfs(root, 0, 0), dfs(root,1, 0))-1; } private int dfs(TreeNode node, int direction, int step){ if(node == null) return step; int max = 0; //1 -> right, 0-> left if(direction==1){ //either you can continue on the same path and take right int a = dfs(node.right, 1-direction, step+1); //or you can start a new path from the current node and go right int b = dfs(node.left, 1, 1); int c = Math.max(a, b); max = Math.max(max, c); } else { //either you can continue on the same path and take left int a = dfs(node.left, 1-direction, step+1); //or you can start a new path from the current node and go left int b = dfs(node.right, 0, 1); int c = Math.max(a, b); max = Math.max(max, c); } return max; } } |