Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at vertex 0 and coming back to this vertex. The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that an edge exists connecting the vertices ai and bi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple; otherwise, it does not have any apples.
https://leetcode.com/problems/minimum-time-to-collect-all-apples-in-a-tree/description/
|
1 2 3 |
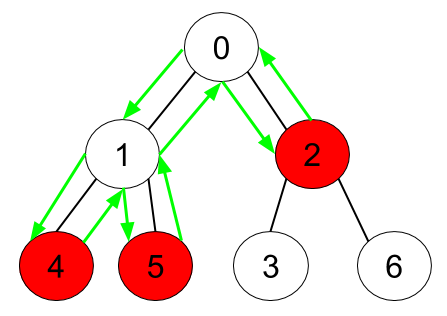
<strong>Input:</strong> n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false] <strong>Output:</strong> 8 <strong>Explanation:</strong> The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows. |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
class Solution { public int minTime(int n, int[][] edges, List<Boolean> hasApple) { //create a graph Map<Integer, List<Integer>> graph = new HashMap<>(); for(int[] edge: edges){ //undirected graph //add edge a->b addEdge(graph, edge[0], edge[1]); //add edge b->a addEdge(graph, edge[1], edge[0]); } //to keep track of the visited node Set<Integer> visited = new HashSet<>(); int totalTime = dfs(graph, 0, -1, visited, hasApple); return totalTime; } //add an edge to graph - represented by an adjacency list private void addEdge(Map<Integer, List<Integer>> graph, int a, int b){ List<Integer> list = graph.getOrDefault(a, new ArrayList<>()); list.add(b); graph.put(a, list); } private int dfs(Map<Integer, List<Integer>> graph, int node, int parent, Set<Integer> visited, List<Boolean> hasApple){ //total time to collect all the apples int totalTime = 0; //time taken to collect all the apples in a subtree int childTime = 0; //if the node is not visited yet if(!visited.contains(node)){ if(graph.containsKey(node)){ //visit all the children of the node for(int adj: graph.get(node)){ //to prevent cycle if(adj!=parent){ childTime=dfs(graph, adj, node, visited, hasApple); //if childTime > 0, there is one or more node with an apple in the subtree //or if the node has apple if(childTime>0 || hasApple.get(adj)){ totalTime = totalTime+childTime+2; } } } } //mark the node as visited visited.add(node); } return totalTime; } } |