Floyd’s Algorithm for shortest path

Based on Dynamic Programming

 

• It is a graph analysis algorithm for finding shortest paths in a weighted graph with positive or negative edge(but without negative cycle)(shortest path between all pairs)
• The single execution of the algorithm will find the lengths(summed weights) of the shortest paths between all pairs of vertices. though it does not return details of the themselves.
• Also used for finding transitive closure

 

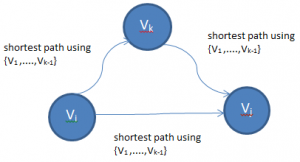
Consider a graph G with vertices V numbered 1 through N. Further consider a function shortestPath(i,j,k) that return the shortest possible path from i to j using vertices only from the set {1,2,3,..,k} as intermediate point along way.

 

shortestPath(i,j,k) : returns shortest path from i to j using vertices from the set {1,2,..,k}

 

Goal: our goal is to find the shortest path from i to j using only vertices from the set {1,2,..,k,k+1}

 

for each of these pair of vertices, the true shortest path could be either

1. a path that only uses vertices from the set {1,..,k}
2. a path that goes from i to k+1 and then from k+1 to j

 

we know the best path from i to j that only uses vertices {1,..,k} is defined by shortestPath(i,j,k) and it is clear that if there were a better path from i to k+1 to j, then the length of this path would be concatenation of the shortest path from i to k+1 using vertices in {1,…,k} and the shortest path from k+1 to j (again, using vertices in {1,…,k})

 

shortestPath(i,j,0) = w(i,j) 

where w(i,j) is weight of vertex from i to j.

and recursive case is